本案例使用 Python 逐步实现了三种基于树的模型:分类回归决策树(CART)、随机森林和 AdaBoost 。在实现的过程中,我们借助 Matplotlib 和 Networkx 等工具对决策树进行了可视化,并使用简单的样例数据对三种算法的表现进行了分析。

目录¶
- 分类决策树 Python 实现
1.1 定义决策树节点
1.2 基尼系数计算
1.3 分类决策树生成
1.4 使用 Networkx 将决策树可视化
1.5 决策树的决策边界
1.6 实现决策树的预测函数
- 回归决策树 Python 实现
2.1 回归树节点实现
2.2 回归决策树生成
2.3 在鲍鱼数据集上测试回归效果
- 实现随机森林算法
- 实现 AdaBoost 算法
- 基于树模型的个人信用风险评估
- 总结
1 分类决策树 Python 实现
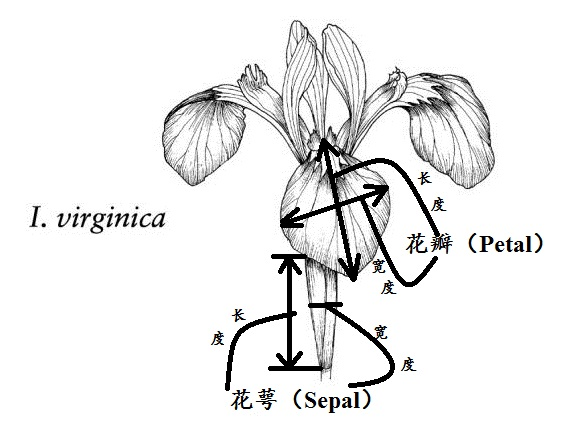
我们首先加载一份鸢尾花数据集以便于测试。鸢尾花数据集包含 150 个鸢尾花样本,每个样本包含 4 个特征和一个类别标签,数据集下载地址为 UCI鸢尾花。在 Sklearn 中可以使用 datasets.load_iris 方法直接加载该数据集。
from sklearn.datasets import load_iris
import pandas as pd
iris = load_iris()
iris_df = pd.DataFrame(data=iris.data,columns=iris.feature_names)
iris_df["target"] = iris.target
iris_df.head()
iris_df.columns = ["sepal_len","sepal_width","petal_len","petal_width","target"]
X_iris = iris_df.iloc[:,:-1]
y_iris = iris_df["target"]
iris_df.head()
下面我们开始实现 CART 决策树算法。首先,我们需要创建一个 TreeNode 类代表决策树的节点。CART 使用基尼系数 (Gini index) 作为不纯度度量,我们随后将实现一个 gini 函数来计算基尼系数。完成节点的定义和基尼系数的计算,我们就可以开始实现决策树的生成算法。为了直观地展示学习到的决策树的结构,我们将借助 Matplotlib 和 Networkx 实现决策树的可视化。
class TreeNode:
def __init__(self,x_pos,y_pos,layer,class_labels=[0,1,2]):
self.f = None #当前节点的切分特征
self.v = None #当前节点的切分点
self.left = None #左儿子节点
self.right = None #右儿子节点
self.pos = (x_pos,y_pos) # 节点坐标,可视化用
self.label_dist = None #当前节点样本的类分布
self.layer = layer
self.class_labels = class_labels
def __str__(self): #打印节点信息,可视化时的节点标签
if self.f != None:
return self.f + "\n<=" + str(round(self.v,2))
else:
return str(self.label_dist) + "\n(" + str(np.sum(self.label_dist)) + ")"
上面的代码中,__str__ 函数定义调用打印函数 print 时输出的信息。对于非叶子节点(判断条件self.f != None),打印节点的特征和切分点;对于叶子节点,打印节点训练样本的类别分布和样本数量。这些信息将在绘制决策树时作为节点的标签信息。
Gini系数是一种度量落在决策树中某一个节点的样本分布不纯度的指标。假设数据集中样本一共有 $C$ 个类别,在节点 $t$ 中第 $c$ 类样本的比例为 $p_{t,c}$,则节点 $t$ 的不纯度为 $$ \text{Gini}(t) = 1 - \sum_{c=1}^C p^2_{t,c} $$ 假设样本的类别为正负两类,假设某个节点一共有 10 个样本,包括 5 个正样本和 5 个负样本,则基尼系数为 $$1 - \left(\frac{5}{10}\right)^2 - \left(\frac{5}{10}\right)^2 = \frac{1}{2}$$ 假设另一个节点有 20 个样本,包含 15 个正样本和 5 个负样本,则基尼系数为
$$1 - \left(\frac{15}{20}\right)^2 - \left(\frac{5}{20}\right)^2 = \frac{3}{8}$$实现一个不纯度计算方法 gini ,它的输入是当前节点样本的标签序列 $y$。 $y$ 是 Pandas 的 Series 结构。我们使用 value_counts 方法计算每一类样本的数量,然后借助 np.square 和 sum 函数计算其平方和。
import numpy as np
def gini(y):
return 1 - np.square(y.value_counts()/len(y)).sum()
下图详细演示了基尼系数的计算过程。

import pandas as pd
gini(pd.Series([1,1,-1,-1,1]))
实现 generate 函数,输入数据子集,输出创建好的节点。其中 X 和 y 分别为训练集特征部分和标签部分,是该函数的主要输入,其余的输入参数为一些辅助参数,其主要含义如下表所示。
| 输入参数 | 含义说明 |
|---|---|
X |
数据子集特征部分,格式为 DataFrame |
y |
数据子集特征部分,格式为 Series |
x_pos |
节点x轴坐标 |
y_pos |
节点y轴坐标 |
nodes |
用户保存决策树中所有节点的列表 |
min_leaf_samples |
叶子节点最少样本数量 |
max_depth |
决策树最大深度 |
layer |
当前节点的层数,等于该节点父节点层数加1 |
class_labels |
样本的标签集合,格式为 Series |
决策树生成函数 generate 的主要流程为:
1 创建当前节点
current_node,计算其样本分布label_dist2 if 当前样本数量太少,决策树层数超过最大深度或者节点的基尼系数小于某个阈值
- 节点不再分裂,返回
current_node
- 节点不再分裂,返回
3 else
3.1 遍历所有候选特征和切分点对 $(f,v)$ ,计算其基尼系数,找出最佳的分裂特征和切分点 $(best\_f,best\_v)$
3.2 根据 $(best\_f,best\_v)$ 将数据子集分为两个子集 $(X1,y1)$ 和 $(X2,y2)$
3.3 使用 $(X1,y1)$ 调用
generate函数创建current_node的左儿子节点3.3 使用 $(X2,y2)$ 调用
generate函数创建current_node的左儿子节点
4 返回当前节点
current_node
def generate(X,y,x_pos,y_pos,nodes,min_leaf_samples,max_depth,layer,class_labels):
current_node = TreeNode(x_pos,y_pos,layer,class_labels)#创建节点对象
current_node.label_dist = [len(y[y==v]) for v in class_labels] #当前节点类样本分布
nodes.append(current_node)
if(len(X) < min_leaf_samples or gini(y) < 0.1 or layer > max_depth): #判断是否需要生成子节点
return current_node
max_gini,best_f,best_v = 0,None,None
for f in X.columns: #特征遍历
for v in X[f].unique(): #取值遍历
y1,y2 = y[X[f] <= v],y[X[f] > v]
if (len(y1) >= min_leaf_samples and len(y2) >= min_leaf_samples):
imp_descent = gini(y) - gini(y1)*len(y1)/len(y) - gini(y2)*len(y2)/len(y) # 计算不纯度变化
if imp_descent > max_gini:
max_gini,best_f,best_v = imp_descent,f,v
current_node.f,current_node.v = best_f,best_v
if(current_node.f != None):
current_node.left = generate(X[X[best_f] <= best_v],y[X[best_f] <= best_v],x_pos-(2**(max_depth-layer)),y_pos -1,nodes,min_leaf_samples,max_depth,layer + 1,class_labels)
current_node.right = generate(X[X[best_f] > best_v],y[X[best_f] > best_v],x_pos+ (2**(max_depth-layer)),y_pos -1,nodes,min_leaf_samples,max_depth,layer + 1,class_labels)
return current_node
为了后续使用方便,我们创建一个封装函数 decision_tree_classifier,其输入为训练数据,叶子节点最小样本数和树的最大深度。返回树的根,节点集合。
def decision_tree_classifier(X,y,min_leaf_samples,max_depth):
nodes = []
root = generate(X,y,0,0,nodes,min_leaf_samples=min_leaf_samples,max_depth=max_depth,layer=1,class_labels=y.unique())
return root,nodes
Networkx 是一个 Python 中流行的网络分析工具,实现了网络的可视化函数。我们将使用该工具的 draw_networkx 函数对生成的决策树进行可视化。draw_networkx 函数需要输入 Networkx 中的网络对象,节点坐标,节点颜色,节点大小等参数,列举如下表所示。
| 参数 | 含义说明 |
|---|---|
G |
Networkx网络对象 |
pos |
指定节点坐标的字典对象,键为节点,值为坐标(x,y) |
ax |
Matplotlib Axes对象,将网络绘制在该子图上 |
node_shape |
节点形状,常见的有圆形("o"),方形("s"),上三角形("^")等 |
font_color |
节点标签字体颜色 |
node_size |
节点大小 |
node_color |
节点颜色 |
编写一个函数,将训练得到的决策树转换成 Networkx 中的网络对象 G。
def get_networkx_graph(G, root):
if root.left != None:
G.add_edge(root, root.left) #在当前节点和左儿子节点之间建立一条边,加入G
get_networkx_graph(G, root.left) #对左儿子执行同样操作
if root.right != None:
G.add_edge(root, root.right) #在当前节点和左儿子节点之间建立一条边,加入G
get_networkx_graph(G,root.right)#对右儿子执行同样操作
在决策树生成函数中,已经计算了节点的坐标。现在我们实现一个函数,输入节点集合,返回其位置布局字典对象。
def get_tree_pos(G):
pos = {}
for node in G.nodes:
pos[node] = node.pos
return pos
在决策树中,如果是叶子节点,则根据其预测类别显示不同颜色。如果是非叶子节点,则显示灰色。
def get_node_color(G):
color_dict = []
for node in G.nodes:
if node.f == None: #叶子节点
label = np.argmax(node.label_dist)
if label%3 == 0:
color_dict.append("#007979") #深绿色
elif label%3 == 1:
color_dict.append("#E4007F") #洋红色
else:
color_dict.append("blue")
else:
color_dict.append("gray")
return color_dict
在鸢尾花数据集上训练决策树,然后将学习到的决策树绘制出来。
import matplotlib.pyplot as plt
import networkx as nx
%matplotlib inline
#1训练决策树
root,nodes = decision_tree_classifier(X_iris,y_iris,min_leaf_samples=10,max_depth=4)
#2将决策树进行可视化
fig, ax = plt.subplots(figsize=(9, 9)) #2.1将图的大小设置为 9×9
graph = nx.DiGraph() #2.2 创建 Networkx 中的网络对象
get_networkx_graph(graph, root) # 2.3 将决策树转换成 Networkx 的网络对象
pos = get_tree_pos(graph) #2.4 获取节点的坐标
# 2.5 绘制决策树
nx.draw_networkx(graph,pos = pos,ax = ax,node_shape="o",font_color="w",node_size=5000,node_color=get_node_color(graph))
plt.box(False) #去掉边框
plt.axis("off")#不显示坐标轴
对于二维数据,我们可以将决策树的决策边界可视化。基本想法是遍历决策树的节点,查看节点的分裂特征和切分点。如果分裂特征对应横轴,则在切分点坐标绘制一条竖线。如果分裂特征对应纵轴,则在切分点绘制一条水平线。下面,我们选取鸢尾花数据集中的 petal_len 和 petal_width 这两个特征,在二维数据集上训练决策树,然后将决策树的决策边界绘制出来。
import seaborn as sns
#筛选两列特征
feature_names = ["petal_len","petal_width"]
X = iris_df[feature_names]
y = iris_df["target"]
#训练决策树模型
tree_two_dimension, nodes = decision_tree_classifier(X,y,min_leaf_samples=10,max_depth=4)
绘制决策边界。
#开始绘制决策边界
fig, ax = plt.subplots(figsize=(9, 9)) #设置图片大小
sns.scatterplot(x = X.iloc[:,0], y = X.iloc[:,1],ax = ax,hue = y) #绘制样本点
#遍历决策树节点,绘制划分直线
for node in nodes:
if node.f == X.columns[0]:
ax.vlines(node.v,X.iloc[:,1].min(),X.iloc[:,1].max(),color="gray") # 如果节点分裂特征是 petal_len ,则绘制竖线
elif node.f == X.columns[1]:
ax.hlines(node.v,X.iloc[:,0].min(),X.iloc[:,0].max(),color="gray") #如果节点分裂特征是 petal_width ,则绘制水平线
同样,为了方便,我们将边界绘制代码封装为一个函数 plot_tree_boundary 。
def plot_tree_boundary(X,y,tree,nodes):
#优化计算每个决策线段的起始点
for node in nodes:
node.x0_min,node.x0_max,node.x1_min,node.x1_max = X.iloc[:,0].min(),X.iloc[:,0].max(),X.iloc[:,1].min(),X.iloc[:,1].max(),
node_list = []
node_list.append(tree)
while(len(node_list)> 0):
node = node_list.pop()
if node.f != None:
node_list.append(node.left)
node_list.append(node.right)
if node.f == X.columns[0]:
node.left.x0_max = node.v
node.right.x0_min = node.v
elif node.f == X.columns[1]:
node.left.x1_max = node.v
node.right.x1_min = node.v
fig, ax = plt.subplots(figsize=(9, 9)) #设置图片大小
sns.scatterplot(x = X.iloc[:,0], y = X.iloc[:,1],ax = ax,hue = y) #绘制样本点
#遍历决策树节点,绘制划分直线
for node in nodes:
if node.f == X.columns[0]:
ax.vlines(node.v,node.x1_min,node.x1_max,color="gray") # 如果是节点分裂特征是 petal_len ,则绘制竖线
elif node.f == X.columns[1]:
ax.hlines(node.v,node.x0_min,node.x0_max,color="gray") #如果是节点分裂特征是 petal_width ,则绘制水平线
#绘制边框
ax.vlines(X.iloc[:,0].min(),X.iloc[:,1].min(),X.iloc[:,1].max(),color="gray")
ax.vlines(X.iloc[:,0].max(),X.iloc[:,1].min(),X.iloc[:,1].max(),color="gray")
ax.hlines(X.iloc[:,1].min(),X.iloc[:,0].min(),X.iloc[:,0].max(),color="gray")
ax.hlines(X.iloc[:,1].max(),X.iloc[:,0].min(),X.iloc[:,0].max(),color="gray")
plot_tree_boundary(X,y,tree_two_dimension,nodes)
下面我们生成一个边界稍微复杂的"环形"随机数据集,来进一步加深对决策树的决策边界的理解。
from sklearn import datasets
# 生成环形图,factor 控制两个环的距离
sample,target = datasets.make_circles(n_samples=1000,shuffle=True,noise=0.2,random_state=0,factor=0.4)
data = pd.DataFrame(data=sample,columns=["x1","x2"])
data["label"] = target
tree_two_dimension,nodes2 = decision_tree_classifier(data[["x1","x2"]],data["label"],min_leaf_samples=10,max_depth=5)
plot_tree_boundary(data[["x1","x2"]],data["label"],tree_two_dimension,nodes2)
生成一份随机分类数据集,查看决策树边界。
from sklearn import datasets
sample,target = datasets.make_classification(n_samples=1000, #样本数量
n_classes=4, #类别数量
n_features=2, #特征数量
n_informative=2,#有信息特征数量
n_redundant=0, #冗余特征数量
n_repeated=0, # 重复特征数量
n_clusters_per_class=1, #每一类的簇数
flip_y=0, # 样本标签随机分配的比例
class_sep=2,#不同类别样本的分散程度
random_state=203)
data = pd.DataFrame(data=sample,columns=["x1","x2"])
data["label"] = target
tree_two_dimension,nodes2 = decision_tree_classifier(data[["x1","x2"]],data["label"],min_leaf_samples=10,max_depth=5)
plot_tree_boundary(data[["x1","x2"]],data["label"],tree_two_dimension,nodes2)
训练得到一个决策树,新到一个样本后,对样本的标签进行预测。我们需要给 TreeNode 类添加一个 predict 方法。如果当前节点是叶子节点,则直接预测最多的类标签。如果当前节点是内部节点,则根据当前样本在节点特征上的取值情况,调用左儿子节点或右儿子节点的 predict 方法。
class TreeNode:
def __init__(self,x_pos,y_pos,layer,class_labels=[0,1,2]):
self.f = None #当前节点的切分特征
self.v = None #当前节点的切分点
self.left = None #左儿子节点
self.right = None #右儿子节点
self.pos = (x_pos,y_pos) # 节点坐标,可视化用
self.label_dist = None #当前节点样本的类分布
self.layer = layer
self.class_labels = class_labels
def __str__(self): #打印节点信息,可视化时的节点标签
if self.f != None:
return self.f + "\n<=" + str(self.v)
else:
return str(self.label_dist) + "\n(" + str(round(np.sum(self.label_dist),2)) + ")"
#对测试样本进行预测
def predict(self,x):
if self.f == None:
return self.class_labels[np.argmax(self.label_dist)]
elif x[self.f] <= self.v:
return self.left.predict(x)
else:
return self.right.predict(x)
再次训练决策树模型。
tree,tree_nodes = decision_tree_classifier(X_iris,y_iris,min_leaf_samples=10,max_depth=4)
选取样本进行测试。
sample = iris_df.iloc[77,:]
y_pred = tree.predict(sample)
print(y_pred,sample["target"])
y_pred = []
for _,sample in iris_df.iterrows():
y_pred.append(tree.predict(sample))
y_pred[:10]
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(9,9))
# 设置正常显示中文
sns.set(font='SimHei')
# 绘制热力图
confusion_matrix = confusion_matrix(y_pred,iris_df["target"])#计算混淆矩阵
ax = sns.heatmap(confusion_matrix,linewidths=.5,cmap="Greens",
annot=True, fmt='d',xticklabels=iris.target_names, yticklabels=iris.target_names)
ax.set_ylabel('真实')
ax.set_xlabel('预测')
ax.xaxis.set_label_position('top')
ax.xaxis.tick_top()
ax.set_title('混淆矩阵热力图')
修改树节点类,与分类决策树的节点中存储不同类样本数量不同的是,在回归决策树的节点中,我们需要保存该节点样本的目标值的均值。在预测方法中,如果当前节点是叶子节点,则直接输出均值进行预测。
class TreeNodeRegression:
def __init__(self,y_mean,num_samples,x_pos,y_pos,layer):
self.f = None #当前节点的切分特征
self.v = None #当前节点的切分点
self.left = None #左儿子节点
self.right = None #右儿子节点
self.pos = (x_pos,y_pos) # 节点坐标,可视化用
self.y_mean = y_mean #节点样本均值
self.num_samples = num_samples #节点的样本数
self.layer = layer
def __str__(self): #打印节点信息,可视化时的节点标签
if self.f != None:
return self.f + "\n<=" + str(round(self.v,2))
else:
return str(round(self.y_mean,2)) + "\n(" + str(self.num_samples) + ")" #修改2********************#
#对测试样本进行预测
def predict(self,x):
if self.f == None:
return self.y_mean #修改3********************#
elif x[self.f] <= self.v:
return self.left.predict(x)
else:
return self.right.predict(x)
在回归决策树中,不纯度的度量是均方误差。修改决策树生成函数。
def generate_regression(X,y,x_pos,y_pos,nodes,min_leaf_samples,max_depth,layer):
current_node = TreeNodeRegression(np.mean(y),len(y),x_pos,y_pos,layer)#创建节点对象
nodes.append(current_node)
if(len(X) < min_leaf_samples): #判断是否需要生成子节点
return current_node
min_square,best_f,best_v = 10e10,None,None #修改1******************#
for f in X.columns: #特征遍历
for v in X[f].unique(): #取值遍历
y1,y2 = y[X[f] <= v],y[X[f] > v]
#修改2******************#
split_error = np.square(y1 - np.mean(y1)).sum()*len(y1)/len(y) + np.square(y2 - np.mean(y2)).sum()*len(y2)/len(y) # 计算当前切分的均方误差
if(split_error < min_square and len(y1) >= min_leaf_samples and len(y2) > min_leaf_samples and layer <= max_depth): #修改3******************#
min_square,best_f,best_v = split_error,f,v
current_node.f,current_node.v = best_f,best_v
if(current_node.f != None):
current_node.left = generate_regression(X[X[best_f] <= best_v],y[X[best_f] <= best_v],x_pos-(2**(max_depth-layer)),y_pos -1,nodes,min_leaf_samples,max_depth,layer + 1)
current_node.right = generate_regression(X[X[best_f] > best_v],y[X[best_f] > best_v],x_pos+(2**(max_depth-layer)),y_pos -1,nodes,min_leaf_samples,max_depth,layer + 1)
return current_node
同理,创建一个封装的决策树回归函数。
def decision_tree_regression(X,y,min_leaf_samples,max_depth):
nodes = []
root = generate_regression(X,y,0,0,nodes,min_leaf_samples=min_leaf_samples,max_depth=max_depth,layer=1)
return root,nodes
我们已经完成了回归决策树的实现,现在使用机器学习第二讲中使用回归模型预测鲍鱼年龄案例中的鲍鱼数据集来进行测试。
abalone = pd.read_csv("./input/abalone_dataset.csv")
abalone["sex"] = abalone["sex"].map({"M":1,"F":2,"I":3})
X_abalone = abalone.iloc[:,:-1]
y_abalone = abalone["rings"]
abalone_tree,nodes = decision_tree_regression(X_abalone,y_abalone,min_leaf_samples=50,max_depth=4)
def get_node_color2(G):
color_dict = []
for node in G.nodes:
if node.f == None:
color_dict.append("#007979") #深绿色 #E4007F
else:
color_dict.append("gray")
return color_dict
%matplotlib inline
fig, ax = plt.subplots(figsize=(20,20))
graph = nx.DiGraph()
get_networkx_graph(graph, abalone_tree)
pos = get_tree_pos(graph)
nx.draw_networkx(graph,pos = pos,ax = ax,node_shape="o",font_color="w",node_size=5000,node_color=get_node_color2(graph),font_size=10)
plt.box(False)
plt.axis("off")
在鲍鱼数据集中,我们构建的回归树的效果怎样呢?我们计算模型在训练集中的平均绝对误差和决定系数 $R^2$ 。
y_abalone_pred = [] #记录预测值
for _,sample in abalone.iterrows():
y_abalone_pred.append(abalone_tree.predict(sample)) #使用回归决策树进行预测
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import r2_score
print("平均绝对误差:",round(mean_absolute_error(abalone["rings"],y_abalone_pred),4))
print("决定系数:",round(r2_score(abalone["rings"],y_abalone_pred),4))
随机森林的基本思想是:随机选择特征和有放回随机抽样与原始样本同等大小的样本,然后在抽样的数据子集上训练决策树。算法的基本流程如下:
1 输入:训练集 $D$ ,特征维度 $d$,随机选取的特征数 $m$,决策树算法 $h$,树的数量 $T$
2 for $t=1,\cdots,T$
2.1 从训练集 $D$ 中有放回地抽样 $n$ 个样本,记为子集 $D_t$
2.2 从 $d$ 个特征中随机选取 $m$ 个特征
2.3 使用决策树算法,使用 $D_t$ 中选择的 $m$ 个特征训练一棵决策树 $h_t(\mathbf{x})$
3 输出:分类:$H(\mathbf{x}) = \text{majority_vote}(\{h_t(\mathbf{x})\}^T_{t=1})$;回归:$H(\mathbf{x})=\frac{1}{T}\sum_{t=1}^{T} h_t(\mathbf{x})$
def random_forest(X,y,num_trees=10,num_features = 10,min_leaf_samples=10,max_depth=5):
trees = []
nodes_list = []
for t in range(num_trees):
#2.1随机生成特征子集
features_sample = np.random.choice(X.columns,num_features,replace=False)
# 有放回地抽样样本
sample_index = np.random.choice(X.index,len(X),replace=True)
#2.2 得到本轮训练数据集
X_sample = X[features_sample].loc[sample_index,:]
y_sample = y[sample_index]
#2.3训练决策树
tree,nodes = decision_tree_classifier(X_sample,y_sample,min_leaf_samples,max_depth)
trees.append(tree)
nodes_list.append(nodes)
return trees,nodes_list #返回树根的集合,以及每棵树的节点集合的列表
我们将通过鸢尾花数据集对随机森林的表现进行分析,首先将鸢尾花数据集随机划分为训练集和测试集。
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X_iris,y_iris,test_size=0.5,stratify=y_iris)
训练随机森林算法,树的数量设置为 10,每棵树随机选择 3 个特征进行训练,决策树最大深度为 3, 叶子节点最小样本数为 10。
trees,nodes_list = random_forest(X_train,y_train,num_trees=10,num_features = 3,min_leaf_samples=10,max_depth=3)
将随机森林的树绘制出来。
%matplotlib inline
fig, ax = plt.subplots(figsize=(30, 30))
for i in range(len(trees)): # 遍历随机森林中的每棵树
plt.subplot(3,4,i+1)
graph = nx.DiGraph()
get_networkx_graph(graph, trees[i]) #将决策树转换成 networkx 网络对象
pos = get_tree_pos(graph)
nx.draw_networkx(graph,pos = pos,node_shape="o",font_color="w",node_size=5000,node_color=get_node_color(graph)) #绘制决策树
plt.box(False)
plt.axis("off")
对于分类问题,随机森林的预测是其中每棵树的预测的投票,我们实现 rf_predict 方法来实现随机森林预测。
def rf_predict(trees,X_test):
results = []
for _,sample in X_test.iterrows():
pred_y = []
for tree in trees:
pred_y.append(tree.predict(sample))
results.append(pd.Series(pred_y).value_counts().idxmax()) #实现投票
return results
这 10 个决策树组成的随机森林算法,效果如何?首先获得随机森林在预测集上的预测结果。
y_test_pred = rf_predict(trees,X_test)
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(9,9))
confusion_matrix = confusion_matrix(y_test_pred,y_test)#计算混淆矩阵
ax = sns.heatmap(confusion_matrix,linewidths=.5,cmap="Greens",
annot=True, fmt='d',xticklabels=iris.target_names, yticklabels=iris.target_names)
ax.set_ylabel('真实')
ax.set_xlabel('预测')
ax.xaxis.set_label_position('top')
ax.xaxis.tick_top()
ax.set_title('混淆矩阵热力图')
训练单个决策树,打印效果。
from sklearn.metrics import confusion_matrix
single_tree,tree_nodes = decision_tree_classifier(X_train,y_train,min_leaf_samples=10,max_depth=3)
y_pred_single_tree = []
for _,sample in X_test.iterrows():
y_pred_single_tree.append(single_tree.predict(sample))
fig, ax = plt.subplots(figsize=(9,9))
confusion_matrix = confusion_matrix(y_pred_single_tree,y_test)#计算混淆矩阵
ax = sns.heatmap(confusion_matrix,linewidths=.5,cmap="Greens",
annot=True, fmt='d',xticklabels=iris.target_names, yticklabels=iris.target_names)
ax.set_ylabel('真实')
ax.set_xlabel('预测')
ax.xaxis.set_label_position('top')
ax.xaxis.tick_top()
ax.set_title('混淆矩阵热力图')
AdaBoost 的基本思想是通过改变样本的权重来串行地训练多个基模型。每个基分类器在权重分布的样本集下进行训练,根据其在训练样本中的加权误差来确定基分类器模型的权重。然后根据基分类器的权重以及对当前样本的预测情况更新样本的权重。算法流程如下:
1 初始化样本权重 $\mathbf{w}^0=(\frac{1}{n},\cdots,\frac{1}{n})$
2 for $t = 1,\cdots,T$
2.1 根据当前样本权重,训练基分类器 $h_t$
2.2 计算 $h_t$ 的加权误差 $\varepsilon_t = \frac{\sum_{i=1}^{n} w_i^t \text{I}(y_i \ne h_t(\mathbf{x}_i))}{\sum_{i=1}^{n} w_i^t}$
2.3 计算 $h_t$ 的权重 $\alpha_t = \frac{1}{2} \ln (\frac{1 - \varepsilon_t}{\varepsilon_t})$
2.4 更新样本权重 $\mathbf{w}^{t+1} \leftarrow \frac{\mathbf{w}^{t} \cdot e^{-\alpha_t y_i h_t({\mathbf{x}_i}})}{Z_t}$
3 返回集成模型 $H(x) = \sum_{t=1}^{T}\alpha_t h_t(\mathbf{x})$
为了简单,我们这里只实现二分类,且假设标签取值为 1 或 -1 。如果使用的基分类器为决策树,需要将决策树算法进行修改,以使得支持设置样本权重。而在决策树中,权重主要影响的是基尼系数的计算。实现函数 gini_with_weight,它用对应分类的样本权重和的比例来代替传统基尼系数中样本数量的比例。
import numpy as np
def gini_with_weight(y,sample_weights):
weights = sample_weights[y.index] #从全量样本权重中,抽取当前样本子集的权重
return 1 - np.square(weights.groupby(y).sum()/weights.sum()).sum() #将权重按照取值进行分组,每一组求和,除以当前样本总权重,再求平方和。
然后,修改 generate 函数。
def generate_with_weights(X,y,x_pos,y_pos,nodes,min_leaf_samples,max_depth,layer,class_labels,sample_weights):
current_node = TreeNode(x_pos,y_pos,layer,class_labels)#创建节点对象
current_node.label_dist = [len(y[y==v]) for v in class_labels] #当前节点类样本分布
nodes.append(current_node)
if(len(X) < min_leaf_samples or gini_with_weight(y,sample_weights) < 0.1 or layer > max_depth): #判断是否需要生成子节点
return current_node
max_gini,best_f,best_v = 0,None,None
for f in X.columns: #特征遍历
for v in X[f].unique(): #取值遍历
y1,y2 = y[X[f] <= v],y[X[f] > v]
if(len(y1) >= min_leaf_samples and len(y2) >= min_leaf_samples):
imp_descent = gini_with_weight(y,sample_weights) - gini_with_weight(y1,sample_weights)*sample_weights[y1.index].sum()/sample_weights[y.index].sum() - gini_with_weight(y2,sample_weights)*sample_weights[y2.index].sum()/sample_weights[y.index].sum() # 计算不纯度变化
if imp_descent > max_gini:
max_gini,best_f,best_v = imp_descent,f,v
current_node.f,current_node.v = best_f,best_v
if(current_node.f != None):
current_node.left = generate_with_weights(X[X[best_f] <= best_v],y[X[best_f] <= best_v],x_pos-(2**(max_depth-layer)),y_pos -1,nodes,min_leaf_samples,max_depth,layer + 1,class_labels,sample_weights)
current_node.right = generate_with_weights(X[X[best_f] > best_v],y[X[best_f] > best_v],x_pos+ (2**(max_depth-layer)),y_pos -1,nodes,min_leaf_samples,max_depth,layer + 1,class_labels,sample_weights)
return current_node
对决策树进行修改以支持样本权重后,现在我们开始实现 AdaBoost 算法。
def adaboost(X,y,num_trees=10,min_leaf_samples=10,max_depth=5):
trees = []
tree_weights = []
# 1 初始化样本权重
sample_weights = pd.Series(data=np.ones_like(y)/len(y),index=y.index)
for t in range(num_trees):
#2.1 使用当前权重训练决策树
nodes = []
tree = generate_with_weights(X,y,0,0,nodes,min_leaf_samples,max_depth,1,[-1,1],sample_weights)
# 2.2 计算当前分类器的误差
#获得预测值
y_pred = []
for _,sample in X.iterrows():
y_pred.append(tree.predict(sample))
y_pred_ts = pd.Series(data=y_pred,index=y.index)
error = sample_weights[y != y_pred_ts].sum()/sample_weights.sum()
# 2.3 根据当前误差,计算当前数的权重
alpha_t = 0.5*np.log((1-error)/error)
# 2.4 更新样本的权重
sample_weights = sample_weights * np.power(np.e,-alpha_t * y_pred_ts * y)
sample_weights = sample_weights/sample_weights.sum()
trees.append(tree)
tree_weights.append(alpha_t)
return trees,tree_weights
我们使用随机数据集,训练由多棵决策树桩组成的 AdaBoost 模型,然后将多个决策树桩的决策边界绘制出来。
from sklearn import datasets
# 生成数据
sample,target = datasets.make_classification(n_samples=20, n_features=2, n_informative=2,n_redundant=0, n_classes=2, n_clusters_per_class=2, scale=7.0,random_state=110)
data = pd.DataFrame(data=sample,columns=["x1","x2"])
data["label"] = target
data["label"] = data["label"].map({0:-1,1:1})
X,y = data.iloc[:,:-1], data["label"]
fig, ax = plt.subplots(figsize=(9, 9)) #设置图片大小
sns.scatterplot(x = X.iloc[:,0], y = X.iloc[:,1],ax = ax,hue = y,s=100) #绘制样本点
adatrees_two_dimension,_ = adaboost(X,y,num_trees=10,min_leaf_samples=2,max_depth=1)
fig, ax = plt.subplots(figsize=(9, 9)) #设置图片大小
sns.scatterplot(x = X.iloc[:,0], y = X.iloc[:,1],ax = ax,hue = y,s=100) #绘制样本点
#绘制划分直线
for tree in adatrees_two_dimension:
if tree.f == "x1":
plt.vlines(tree.v,data["x2"].min(),data["x2"].max(),color="gray") # 如果是节点分裂特征是 x1 ,则绘制竖线
elif tree.f == "x2":
plt.hlines(tree.v,data["x1"].min(),data["x1"].max(),color="gray") #如果是节点分裂特征是 x2 ,则绘制水平线
现在,我们实现 AdaBoost 的预测函数 adaboost_predict。
def adaboost_predict(trees,weights,X_test):
results = []
for _,sample in X_test.iterrows():
pred_y_sum = 0
for t in range(len(trees)):
pred_y_sum += trees[t].predict(sample)*weights[t] #每棵树的预测值的加权和
results.append(1 if pred_y_sum >= 0 else -1)
return results
在个人信用风险评估问题上测试我们实现的算法。
credit = pd.read_csv("./input/credit-data.csv")
print(credit.columns)
credit.columns = ["sd","ruoul","age","due30-50","debt_ratio","income","loan_num","num_90due","num_rlines","due60-89","num_depents"]
credit["sd"] = credit["sd"].map({1:1,0:-1})
credit["sd"].value_counts()
可见正负样本严重不均衡,我们从正负类样本中随机抽取部分样本。
X_neg_samples = credit[credit["sd"] == -1].sample(300)
credit_new = pd.concat([X_neg_samples,credit[credit["sd"] == 1].sample(300)])
credit_new.sample(10)
from sklearn.model_selection import train_test_split
X_credit = credit_new.iloc[:,1:]
y_credit = credit_new["sd"]
X_credit_train,X_credit_test,y_credit_train,y_credit_test = train_test_split(X_credit,y_credit,test_size = 0.2)
5.1 训练决策树、随机森林和 AdaBoost 模型¶
#训练决策树
credit_tree,tree_nodes = decision_tree_classifier(X_credit_train,y_credit_train,min_leaf_samples=50,max_depth=8)
将生成的决策树可视化。
%matplotlib inline
fig, ax = plt.subplots(figsize=(10, 10))
graph = nx.DiGraph()
get_networkx_graph(graph, credit_tree)
pos = get_tree_pos(graph)
nx.draw_networkx(graph,pos = pos,ax = ax,node_shape="o",font_color="w",node_size=5000,node_color=get_node_color(graph),font_size=10)
plt.box(False)
plt.axis("off")
#训练随机森林
credit_rf_trees,_ = random_forest(X_credit_train,y_credit_train,num_trees=10,num_features = 4,min_leaf_samples=30,max_depth=3)
#训练AdaBoost
credit_ada_trees,credit_ada_weights = adaboost(X_credit_train,y_credit_train,num_trees=10,min_leaf_samples=30,max_depth=3)
5.2 三种模型效果的评估¶
使用正确率作为评价指标,查看训练的模型在测试集上的效果。
credit_tree_pred = []
for _,sample in X_credit_test.iterrows():
credit_tree_pred.append(credit_tree.predict(sample))
credit_rf_pred = rf_predict(credit_rf_trees,X_credit_test)
credit_ada_pred = adaboost_predict(credit_ada_trees,credit_ada_weights,X_credit_test)
from sklearn.metrics import accuracy_score
print(round(accuracy_score(y_credit_test,credit_tree_pred),2))
print(round(accuracy_score(y_credit_test,credit_rf_pred),2))
print(round(accuracy_score(y_credit_test,credit_ada_pred),2))
在本案例中,我们使用 Python 分别实现了分类决策树、回归决策树、随机森林和 AdaBoost 算法。在实践中,我们分别使用了 Matplotlib,Seaborn 和 Networkx 等 Python 工具实现数据的可视化和决策树的可视化。数据的预处理使用的主要是 Pandas 包。本案例的目的是通过动手实践,加深对决策树、随机森林和 AdaBoost 算法的理解。案例中的代码实现并不是性能最优的,仅供参考。