PageRank 是谷歌公司起家的算法,在数据科学领域具有重要的地位和作用。PageRank 算法最初提出来用于利用网页之间的链接关系来对网页进行排序,从而优化搜索引擎的效果。如今,我们可以将 PageRank 算法用作网络中节点排序的一般算法。
在本案例中,我们使用一个全球机场之间航线的网络数据集,借助 Python 中的复杂网络分析库 networkx 中实现的 PageRank 算法,完成对全球机场的排序。
1 数据集介绍¶
文件 ./input/out.opsahl-openflights.csv 中的有向网络包含世界各机场之间的航班。有向边表示从一个机场到另一个机场的飞行航线。这个数据集是从Openflights.org 数据中提取出来的,与 Tore Opsahl 在数据集列表中的网络14c相对应,来源网址为:toreopsahl.com。
利用 networkx 中的 read_edgelist 函数,将网络加载到内存中。注意,由于我们处理的是有向网络,所以需要将 create_using 参数设置为 nx.DiGraph()。
import networkx as nx
flights_network = nx.read_edgelist("./input/out.opsahl-openflights.csv",create_using=nx.DiGraph())
print("航班数:" + str(len(flights_network.nodes)))
print("航线数:" + str(len(flights_network.edges)))
在这个航线网络中,一共包含 2939 个机场,30501 条航线。下面我们使用 nx.draw 函数,将网络进行可视化。
import matplotlib.pyplot as plt
%matplotlib inline
fig, ax = plt.subplots(figsize=(24, 16))
pos_flights = nx.kamada_kawai_layout(flights_network) #网络布局
ax.axis("off")
plt.box(False)
nx.draw(flights_network, node_size=30,node_color = "green", edge_color = "#D8D8D8",width=.3, ax=ax)
2 找出最大连通子图¶
从上图中很容易看出,这个网络不是一个连通图。我们从航线网络中提取出最大连通子图进行进一步分析。 对于有向网络, networkx 中的 weakly_connected_component_subgraphs 函数可以返回网络中的连通子图列表。我们只提取最大连通子图。
largest_component = max(nx.weakly_connected_component_subgraphs(flights_network), key=len)#找出最大连通子图
print("航班数:" + str(len(largest_component.nodes)))
print("航线数:" + str(len(largest_component.edges)))
在最大连通子图中,一共包含 2905 个机场和 30442 条航线。下面将最大连通子图进行可视化。
fig, ax = plt.subplots(figsize=(24, 16))
pos_flights2 = nx.kamada_kawai_layout(largest_component)
ax.axis("off")
plt.box(False)
nx.draw(largest_component, node_size=30,node_color = "green", edge_color = "#D8D8D8",width=.3,pos = pos_flights2, ax=ax)
3 PageRank 算法简介¶
PageRank算法是由谷歌创始人拉里·佩奇(Larry Page)和谢尔盖·布林(Sergey Brin)所设计出来的谷歌搜索引擎上的页面排序算法,最早作为论文发表于 1998 年。 论文发表之后没多久,佩奇和布林就以此论文为基础创立了谷歌公司。
PageRank是一个迭代算法。 在初始的时候,每个点的PageRank值都设置成$\frac{1}{|V|}$,其中$|V|$为图中点的数量。 在每一轮的迭代中,每个点 $v$ 都沿着它的出边往它每个邻居点传递 $v$ 的 $\frac{1}{|\text{N}^{+}(v)}|$ 的PageRank值。 于是,经过第 $t+1$ 轮迭代之后,每个点 $v$ 的PageRank值可以表示为 $$ \text{PR}(v,t+1)=\frac{1-\beta}{|V|}+\beta\sum\limits_{u\in N^{-}(v)}\frac{\text{PR}(u,t)}{|N^{+}(u)|} . $$ 其中 $N^{-}(v)$ 为指向节点$v$的节点集合,而 $N^{+}(u)$ 表示 $u$ 指向的节点的集合。
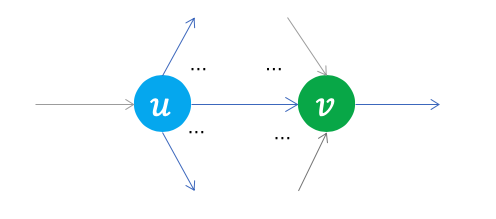
阻尼系数 $\beta$ 用来表示在PageRank迭代过程中一个点沿着出边跳转到下一个点的概率。 $(1 - \beta)$ 表示在浏览过程不沿着边跳转,而是在所有点中随机挑选下一个点的概率。 实际试验证明 $\beta$ 被设置成 $0.85$ 时 PageRank 的计算结果最符合实际情况。
4 使用 PageRank 算法对机场进行排序¶
在 networkx 中,使用 pagerank 函数即可计算网络中节点的 PageRank 值。
pr_dict = nx.pagerank(largest_component)
import pandas as pd
pr_df = pd.DataFrame.from_dict(pr_dict,orient="index")
pr_df.columns = ["pr_value"]
pr_df.sort_values(by = "pr_value").head(20)
pr_df.head(20)
5 将节点大小与 PageRank 值关联并可视化¶
实现一个函数 get_nodesize_pagerank ,将网络中节点的 PageRank 值,映射为网络中节点的大小。
def get_nodesize_pagerank(pagerank, min_size, max_size):
nodesize_list = []
pr_max = max(pagerank.values())
for node, pr in pagerank.items():
nodesize = (max_size - min_size)*pr/pr_max + min_size
nodesize_list.append(nodesize)
return nodesize_list
fig, ax = plt.subplots(figsize=(24, 16))
pos_flights2 = nx.kamada_kawai_layout(largest_component)
ax.axis("off")
plt.box(False)
nx.draw(largest_component, node_size=get_nodesize_pagerank(pr_dict,1,100),node_color = "green", edge_color = "#D8D8D8",width=.3,pos = pos_flights2, ax=ax)