如何用网络来表示人之间的接触关系?在接触网络中,如何通过 SIR 模型模拟疫情的发展趋势?
本案例将介绍SIR模型,图和网络的基本知识。然后使用 NetworkX 工具,在生成的随机网络和真实的网络数据上,实现网络中的 SIR 模型进行疫情模拟。
1 SIR 模型介绍¶
SIR 模型用于计算封闭人群中随着时间推移感染传染性疾病的人数。最早提出来解释在瘟疫(1665-1666年伦敦,1906年孟买)和霍乱(1865年伦敦)等流行病中观察到的感染病人数量的迅速上升和下降。

它假定人口规模是固定的(即无出生和自然死亡等)。传染源的潜伏期是瞬时的,传染持续时间与疾病的长度相同。人群是没有结构的,人之间的接触是完全随机的。恢复之后即获得免疫力,不会继续染病。
1.1 SIR 模型¶
SIR 是传染病中最基础最核心的模型,可以使用下面的图形来表示。

如图所示,在 SIR 模型中,人群被划分为以下三类:
- 易感者(Susceptible):未感染人群,与感染者接触后可能感染疾病,记为 $S(t)$ 或 $S$;
- 感染者(Infectives):感染人群,感染者可能将疾病传染给易感者,也会以一定概率恢复健康,记为 $I(t)$ 或 $I$;
- 恢复者(Recovered):感染后恢复健康的人,在可能致死的疾病中,也可能包括死亡人群,记为 $R(t)$ 或 $R$。
SIR 模型包括两个重要的参数:感染率 $\beta$,指易感者与感染者接触后染病的概率;恢复率 $\gamma$,指感染者恢复的概率。
在某个时间点,多少人会不幸染病呢?SIR 模型假设人之间的接触是随机的,人群中感染者数量是$I$,那么接触到一个感染者的概率是 $\frac{I}{N}$。与感染者接触也不是百分百就会染病,还存在一定概率 $\beta$ 。当前易感人数为 $S$,则会有 $S\frac{I}{N}\beta$ 的人不幸染病。写成方程如下: $$ \frac{{\rm d} S }{{\rm d} t} = - \beta \frac{I}{N} S . $$
SIR 模型中,感染者恢复的概率是 $\gamma$,因此在某个时间点,恢复者的变化如下: $$ \frac{{\rm d} R }{{\rm d} t} = \gamma I . $$
SIR 假设人群总数不变,即 $S + I + R = N$,$N$ 为常数,则在某个时间点,感染者的变化等于减少的易感者减去增加的恢复者,即 $$ \frac{{\rm d} I }{{\rm d} t} = \beta \frac{I}{N} S - \gamma I . $$
可以看到,SIR 模型可以表示成一个常微分方程组:
$$ \left\{ \begin{aligned} \frac{{\rm d} S }{{\rm d} t} &= - \beta \frac{I}{N} S, \\ \frac{{\rm d} I }{{\rm d} t} &= \beta \frac{I}{N} S - \gamma I, \\ \frac{{\rm d} R }{{\rm d} t} &= \gamma I. \end{aligned} \right . $$1.2 使用 Scipy 求解 SIR 模型¶
上述常微分方程组要直接得到解析解(即把 $S,I,R$ 分别直接写成时间 $t$ 的函数)是相当困难的。我们需要使用数值计算的方法。 Scipy 是 Python 中一个做数值计算的包,我们使用这个包来求解上述方程组。首先,定义一个函数 SIR 来表示 SIR 模型。
def SIR(y,t,beta,gamma):
S,I,R = y
dSdt = - S*(I / (S + I + R))*beta
dIdt = beta*S*I/(S + I + R) - gamma*I
dRdt = gamma*I
return [dSdt,dIdt,dRdt]
接下来我们就开始运用 scipy.integrate.odeint() 函数,获得微分方程组的解。
seed = 123 #本案例中将会使用的随机数种子
days = 100 #设置模拟的天数
beta = 0.30 #感染率
gamma = 0.10 #恢复率
N = 150 #人群大小
I0 = 1 #初始感染人数
R0 = 0 #初始恢复人数
S0 = N - I0 - R0
# 设置初始值
y0 = [S0, I0, R0]
from scipy.integrate import odeint
# 求解
solution = odeint(SIR, y0, range(0,days), args = (beta, gamma))
将模拟的结果使用matplotlib工具绘制出来,这里我们直接使用DataFrame对象封装的plot方法。
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
solution_df = pd.DataFrame(solution, columns = ["S","I","R"])
#设置不同人群的显示颜色,易感者为橘色,感染者为红色,恢复者为绿色
color_dict = {"S":"orange","I":"red","R":"green"}
solution_df.plot(figsize=(9,6),color=[color_dict.get(x) for x in solution_df.columns])
为了更好的演示效果,我们使用pyecharts将图动态地演示出来。
from pyecharts.charts import Line, Grid
import pyecharts
import pyecharts.options as opts
SIR_line = Line().add_xaxis(xaxis_data = solution_df.index)
for col in solution_df.columns:
print(col, color_dict[col])
SIR_line.add_yaxis(series_name = col,
y_axis = solution_df[col].values, # 添加数据
symbol_size = 3,
symbol = 'none',
label_opts = opts.LabelOpts(is_show = False),
linestyle_opts = opts.LineStyleOpts(width = 1.5, color = color_dict[col]), # 设置线宽
is_smooth = True)
SIR_line.set_global_opts(axispointer_opts = opts.AxisPointerOpts(is_show = True,
link = [{"xAxisIndex": "all"}]),# 设置坐标轴指示器
legend_opts = opts.LegendOpts(is_show = False))
# 在notebook中进行渲染
SIR_line.render_notebook()
2 网络中的SIR模型¶
网络可以表示成图$G=(V,E)$,其中$V$是节点集合,$E$表示边集合,其中每条边由$V$中两个点相连接所构成。 如果将人之间的接触关系表示成图,那么图中的节点表示人,边则表示人之间的接触关系。不难想象,如果一个人与他人的接触越多,则在图中该节点与其他节点连接的边也会越多。
在 SIR 模型中,假设人之间是随机接触的。如果人之间的接触关系不是随机的,而是形成了一个接触网络。那么在这个网络中,每个人接触到感染者的概率不再相等,而与他在网络中的位置相关。
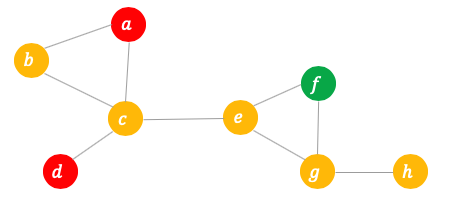
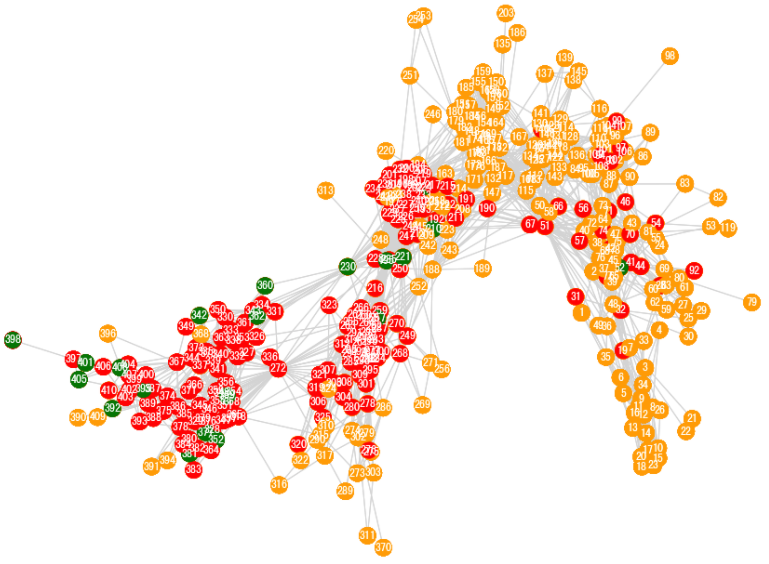
如上图的例子,人群中一共有8个人,其中 $a$ 和 $d$ 是感染者,$f$ 是恢复者,其余人是易感者。在传统的 SIR 模型中,每个易感者接触到感染者的概率一样,为 $\frac{I}{N}=\frac{2}{8}=0.25$。然而,从上图显示的网络中,我们可以很直观地看到,$c$ 接触到感染者的概率远远大于 $h$,因此其染病的概率也会高一些。可见,网络中的 SIR 模型跟网络中节点当前所处的环境息息相关。
与传统 SIR 模型类似,网络中的 SIR 模型也有两个重要的参数:感染率 $\beta$ 和恢复率 $\gamma$。我们需要给每个节点引入一个状态,取值为 S,I,R 中的一种。 每一个时间步中,需要动态对每一个节点的状态进行更新。更新规则如下:
- 如果当前节点是恢复者,则下一步,节点状态依然是恢复者。

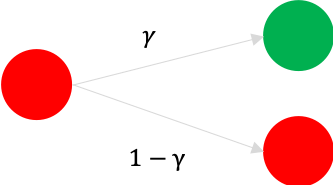
- 如果当前节点是感染者,则下一步,$\gamma$ 的概率转化为恢复者。$1 - \gamma$ 的概率依然是感染者。
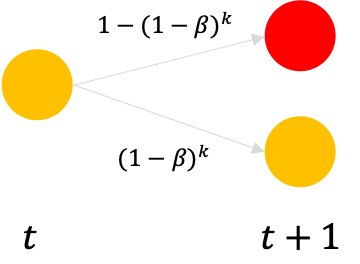
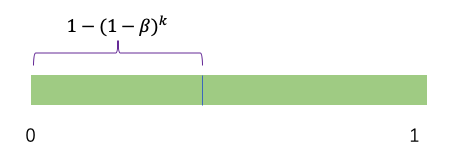
- 如果当前节点是易感者,则需要计算其邻居节点中感染者的数量,假设其有 $k$ 个邻居为感染者。则该节点下一步转化为感染者的概率为 $1 - (1 - \beta)^k$,否则继续保持易感者状态。
对于本次新冠病毒肺炎疫情,如果要使用以上网络的方法对疫情进行模拟,我们还需要构建一个人之间的接触网络。从新闻的疫情报道以及本系列案例中第一次用爬虫抓取的数据,是完全不足以构建接触网络的。需要更多的数据,而这在当前阶段是十分困难的。
本案例中我们采用两种办法简单地构建一个网络结构:使用随机图生成算法生成一个无标度网络;使用一个真实的小型人群接触网络数据集。
3 生成无标度网络进行 SIR 疫情模拟¶
3.1 无标度网络¶
统计物理学家把服从幂律分布的现象称为无标度现象,即系统中个体的尺度相差悬殊,缺乏一个优选的标度。于是,满足幂律分布的网络也被称为无标度网络(scale-free network)。
无标度网络中,节点的度 $d$ 满足以下分布: $$ p(d) \sim d^{-\alpha}. $$ 其中 $\alpha$ 为幂律指数,取值一般在2到3之间。
匈牙利科学家 Barabási 和 Albert 提出了一个 BA 模型(Barabási–Albert model)来生成无标度网络。 BA 模型整体流程如下:
- 首先,初始化$m_0$个相互连通的点;
- 然后,逐个地增加点,每增加一个点,这个新增的点与已有的点相连的概率正比于已有的点的度数。形式化地来说,对于点 $i$ 而言,在新增的点与 $i$ 之间增加一条边的概率 $p_i$ 为 $$ \begin{aligned} p_i=\frac{\text{deg}(i)}{\sum_j \text{deg}(j)} , \end{aligned} $$ 其中 $\text{deg}(i)$ 是点$i$的度数,而 $\sum_j \text{deg}(j)$ 是已有的点度数之和.
3.2 使用 NetworkX 生成无标度网络¶
Python 中的 NetworkX 包提供了方便的随机网络生成函数。其中 barabasi_albert_graph 函数实现了 BA 模型生成无标度网络。主要的参数有网络节点数 $m$ 和新加节点的边数 $n$。在我们的场景中,第二个参数的含义是一个人平均与多少人接触。NetworkX 包还提供了一系列将网络可视化的函数,能够方便地观察网络的结构。我们这里使用 draw_networkx 函数,它的常用参数包括网络对象、是否显示节点标签(with_labels)、网络的布局(pos)等。
#生成100个节点的BA无标度网络
import warnings
warnings.filterwarnings("ignore")
import networkx as nx #导入NetworkX包,命名为nx
random_network = nx.barabasi_albert_graph(100,2) # 生成无标度网络,节点数和每个节点边数分别为100和2
#网络可视化
nx.draw_networkx(random_network,with_labels = True,pos = nx.spring_layout(random_network,seed = 1))
3.3 SIR 疫情模拟与分析¶
节点状态模拟更新函数 updateNodeState¶
我们使用一个简单的函数来实现一个节点的状态的更新。首先,如果一个节点是恢复者,那么下一步还是恢复者,其节点状态保持不变。 如果一个节点是感染者,那么其恢复的概率是 $\gamma$。用程序实现的方法为,先均匀生成一个0到1的随机数 $p$,如果 $p < \gamma$,则节点恢复,否则节点依然处于感染状态。

如果一个节点是易感者,先要去其邻居节点中看看一共有多少个邻居是感染者,有 $k$ 个邻居是感染者,那么当前节点被感染的概率是 $1 - (1 - \beta)^k$。我们生成一个0到1的随机数 $p$,如果 $p < 1 - (1 - \beta)^k$,则节点被感染,否则不被感染。
updateNodeState 函数实现如下所示,其中输入的参数为网络 $G$,节点 $node$,以及 SIR 模型的参数 $\beta$ 和 $\gamma$。
import random
# 根据 SIR 模型,更新节点的状态
def updateNodeState(G,node, beta, gamma):
if G.nodes[node]["state"] == "I": #感染者
p = random.random() # 生成一个0到1的随机数
if p < gamma: # gamma的概率恢复
G.nodes[node]["state"] = "R" #将节点状态设置成“R”
elif G.nodes[node]["state"] == "S": #易感者
p = random.random() # 生成一个0到1的随机数
k = 0 # 计算邻居中的感染者数量
for neibor in G.adj[node]: # 查看所有邻居状态,遍历邻居用 G.adj[node]
if G.nodes[neibor]["state"] == "I": #如果这个邻居是感染者,则k加1
k = k + 1
if p < 1 - (1 - beta)**k: # 易感者被感染
G.nodes[node]["state"] = "I"
网络中所有节点状态模拟更新函数 updateNetworkState¶
有了单个节点状态更新的函数,为了便于后续使用,我们再实现一个整个网络状态进行更新的函数。
def updateNetworkState(G, beta, gamma):
for node in G: #遍历图中节点,每一个节点状态进行更新
updateNodeState(G,node, beta, gamma)
为了动态地追踪易感者、感染者和恢复者数量,我们实现一个函数 countSIR 统计三类人群的数量。
# 计算三类人群的数量
def countSIR(G):
S = 0;I = 0
for node in G:
if G.nodes[node]["state"] == "S":
S = S + 1
elif G.nodes[node]["state"] == "I":
I = I + 1
return S,I, len(G.nodes) - S - I
为了更清楚地演示在网络中疾病的传播过程,我们分别将图中的节点使用不同的颜色进行展示。易感者为橘色,感染者为红色,恢复者为绿色。
def get_node_color(G): #返回每一个节点的颜色组成的列表
color_list = []
for node in G:
#使用我们前面创建的状态到颜色的映射字典 color_dict
color_list.append(color_dict[G.nodes[node]["state"]])
return color_list
在正式开始模拟之前,我们需要进行一些初始化工作,包括节点状态的初始化和 SIR 模型的参数 $\beta$ 和 $\gamma$ 的初始化。
ba = nx.barabasi_albert_graph(N,2,seed=seed)
#初始化节点 state 属性
for node in ba:
ba.nodes[node]["state"] = "S"
#随机选取一个节点为初始感染者
ba.nodes[55]["state"] = "I"
在图中开始 SIR 模型的模拟。设置模拟天数,开始执行模拟过程。
# 模拟天数为days,更新节点状态
import matplotlib.pyplot as plt
#fig,ax = plt.subplots(111)
%matplotlib inline
SIR_list = []
for t in range(0,days):
updateNetworkState(ba,beta,gamma) #对网络状态进行模拟更新
SIR_list.append(list(countSIR(ba))) #计算更新后三种节点的数量
对模拟的结果进行可视化,查看易感者、感染者和恢复者人数的变化趋势。
df = pd.DataFrame(SIR_list,columns=["S","I","R"])
df.plot(figsize=(9,6),color=[color_dict.get(x) for x in df.columns])
我们再次画出在相同的 $\beta$ 和 $\gamma$ 参数,相同的 $S_0,I_0,R_0$ 下,传统 SIR 模型的结果。
solution_df.plot(figsize=(9,6),color=[color_dict.get(x) for x in solution_df.columns])
对比两张图,可以看到,在网络中,疫情发展更为迅猛,最高峰的感染人数也远远高于传统 SIR 模型的模拟结果。为什么呢?作为一个开放性的问题,留给大家自己去想吧。
上面的疫情模拟中展示了每一天不同人群的变化,那么在网络中每一天到底是哪些人感染了?我们可以通过 NetworkX 提供的网络可视化工具深入地分析。通过 networkx.draw_networkx 函数可以方便地将图画出来。
nx.draw_networkx(ba,with_labels = True, node_color = get_node_color(ba), pos = nx.spring_layout(ba,seed = 1))
默认的展示并不是很清晰,我们需要一些额外的设置,例如标签颜色,去掉图片边框,去掉坐标轴刻度,重新设置图的大小等。
fig, ax = plt.subplots(figsize=(9, 6)) #将图的大小设置为 9×6
pos = nx.spring_layout(ba,seed = 1) #设置网络布局,将 seed 固定为 1
ax.axis("off") #关闭坐标轴
plt.box(False) #不显示方框
nx.draw(ba,with_labels = True,font_color="white",node_color = get_node_color(ba), edge_color = "#D8D8D8",pos = pos, ax=ax)
将每一天的节点状态以动画演示。我们借助 matplotlib 包中的动画模块 animation 来实现这一效果。
#运行出结果大概需要90秒
#初始化节点 state 属性
for node in ba:
ba.nodes[node]["state"] = "S"
ba.nodes[55]["state"] = "I"
#绘制网络节点颜色
fig, ax = plt.subplots(figsize=(9, 6))
def graph_draw(i,G,pos,ax,beta,gamma): ## 实现动画中每一帧的绘制函数,i为第几帧
ax.axis("off")
ax.set_title("day " + str(i) + " 黄色(易感者),红色(感染者),绿色(恢复者)")
plt.box(False)
if i == 0: #第一帧,直接绘制网络
nx.draw(G,with_labels = True, font_color="white", node_color = get_node_color(G), edge_color = "#D8D8D8",pos = pos, ax=ax)
else: # 其余帧,先更新网络状态,再绘制网络
updateNetworkState(G, beta, gamma)
nx.draw_networkx_nodes(G, with_labels = True, font_color="white", node_color = get_node_color(G),pos = pos, ax=ax)
plt.close()
#演示网络动态变化
import matplotlib.animation as animation
from IPython.display import HTML
animator = animation.FuncAnimation(fig, graph_draw, frames= range(0,days),fargs=(ba,pos,ax,beta,gamma), interval=200)
HTML(animator.to_jshtml())